Droz-Farny doğru teoremi

Öklid geometrisinde, Droz-Farny doğru teoremi, keyfi bir üçgenin yükseklik merkezinden (ortosantr) geçen iki dik doğrunun bir özelliğidir.

${\displaystyle T}$, köşeleri ${\displaystyle A}$, ${\displaystyle B}$ ve ${\displaystyle C}$ olan bir üçgen ve ${\displaystyle H}$, yükseklik merkezi (üç yüksekliğin kesiştiği ortak nokta) olsun. ${\displaystyle L_{1}}$ ve ${\displaystyle L_{2}}$, ${\displaystyle H}$ üzerinden geçen birbirine dik herhangi iki doğru olsun. ${\displaystyle A_{1}}$, ${\displaystyle B_{1}}$ ve ${\displaystyle C_{1}}$ sırasıyla ${\displaystyle L_{1}}$'in ${\displaystyle BC}$, ${\displaystyle CA}$ ve ${\displaystyle AB}$ kenar doğrularıyla kesiştiği noktalar olsun. Benzer şekilde, ${\displaystyle A_{2}}$, ${\displaystyle B_{2}}$ ve ${\displaystyle C_{2}}$ de ${\displaystyle L_{2}}$'nin bu kenar doğrularıyla kesiştiği noktalar olsun. Droz-Farny doğru teoremi, üç doğru parçası ${\displaystyle A_{1}A_{2}}$,${\displaystyle B_{1}B_{2}}$ ve ${\displaystyle C_{1}C_{2}}$'nin orta noktalarının eşdoğrusal olduğunu ifade eder.^[1][2][3]

Teorem, Arnold Droz-Farny tarafından 1899'da^[1] dile getirilmiştir ancak bir kanıtı olup olmadığı net değildir.^[4]

Droz-Farny doğru teoreminin bir genellemesi 1930'da René Goormaghtigh tarafından kanıtlandı.^[5]

Yukarıdaki gibi ${\displaystyle T}$, köşeleri ${\displaystyle A}$,${\displaystyle B}$ ve ${\displaystyle C}$ olan bir üçgen olsun. ${\displaystyle P}$, ${\displaystyle A}$, ${\displaystyle B}$ ve ${\displaystyle C}$'den farklı herhangi bir nokta olsun ve ${\displaystyle L}$, ${\displaystyle P}$ üzerinden geçen herhangi bir doğru olsun. ${\displaystyle A_{1}}$, ${\displaystyle B_{1}}$ ve ${\displaystyle C_{1}}$ sırasıyla ${\displaystyle BC}$, ${\displaystyle CA}$ ve ${\displaystyle AB}$ kenar doğruları üzerindeki, ${\displaystyle PA_{1}}$, ${\displaystyle PB_{1}}$ ve ${\displaystyle PC_{1}}$ ${\displaystyle L}$ doğrusuna göre simetrik (yansıtma yoluyla) sırasıyla ${\displaystyle PA}$, ${\displaystyle PB}$ ve ${\displaystyle PC}$ doğrularının görüntüleri olacak şekilde noktalar olsun. Daha sonra Goormaghtigh teoremi ${\displaystyle A_{1}}$, ${\displaystyle B_{1}}$ ve ${\displaystyle C_{1}}$ noktalarının eşdoğrusal olduğunu söyler.

Droz-Farny doğru teoremi, ${\displaystyle P}$, ${\displaystyle T}$ üçgeninin yükseklik merkezi olduğunda bu sonucun özel bir durumudur.

Teorem, Dao Thanh Oai tarafından daha da genelleştirildi. Genelleme aşağıdaki gibidir:

İlk genelleme: ${\displaystyle ABC}$ bir üçgen olsun, ${\displaystyle P}$ düzlemdeki bir nokta olsun, üç paralel doğru parçası ${\displaystyle AA',BB',CC'}$ olsun, böylece orta noktalar ve ${\displaystyle P}$ eşdoğrusal olsun. Daha sonra ${\displaystyle PA',PB',PC'}$ sırasıyla üç eşdoğrusal noktada ${\displaystyle BC,CA,AB}$ ile kesişir.^[6]

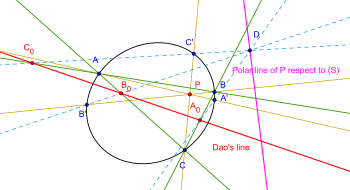
İkinci genelleme: Düzlemde bir konik ${\displaystyle S}$ ve bir ${\displaystyle P}$ noktası olsun. Konik ile sırasıyla ${\displaystyle A,A'}$; ${\displaystyle B,B'}$; ${\displaystyle C,C'}$ noktasında kesişecek şekilde, ${\displaystyle P}$'den geçen üç ${\displaystyle d_{a},d_{b},d_{c}}$ doğrusu oluşturun. ${\displaystyle D}$, (${\displaystyle S}$)'ye göre ${\displaystyle P}$ noktasının kutup doğrusu üzerinde bir nokta olsun veya ${\displaystyle D}$ konik (${\displaystyle S}$) üzerinde yer alır. ${\displaystyle DA'\cap BC=A_{0}}$; ${\displaystyle DB'\cap AC=B_{0}}$; ${\displaystyle DC'\cap AB=C_{0}}$ olsun. O zaman ${\displaystyle A_{0},B_{0},C_{0}}$ eşdoğrusaldır.^[7][8][9]

1. ^ ^{a b} A. Droz-Farny (1899), "Question 14111", The Educational Times, 71, ss. 89-90 
2. ^ Ayme, Jean-Louis (2004), "A Purely Synthetic Proof of the Droz-Farny Line Theorem", Forum Geometricorum, 14, ss. 219-224, ISSN 1534-1178, 16 Temmuz 2020 tarihinde kaynağından arşivlendi 
3. ^ Floor van Lamoen; Eric W. Weisstein, "Droz-Farny Theorem", MathWorld, 27 Ekim 2020 tarihinde kaynağından arşivlendi 
4. ^ O'Connor, John J.; Robertson, Edmund F., "Droz-Farny doğru teoremi", MacTutor Matematik Tarihi arşivi 
5. ^ René Goormaghtigh (1930), "Sur une généralisation du théoreme de Noyer, Droz-Farny et Neuberg"", Mathesis, cilt 44, s. 25 
6. ^ Son Tran Hoang (2014), "A synthetic proof of Dao's generalization of Goormaghtigh's theorem", Global Journal of Advanced Research on Classical and Modern Geometries, cilt 3, ss. 125-129, ISSN 2284-5569, 6 Ekim 2014 tarihinde kaynağından arşivlendi 
7. ^ Nguyen Ngoc Giang, A proof of Dao theorem, Global Journal of Advanced Research on Classical and Modern Geometries, Vol.4, (2015), Issue 2, page 102-105 6 Ekim 2014 tarihinde Wayback Machine sitesinde arşivlendi., ISSN 2284-5569
8. ^ Smith, Geoff (2015). "99.20 A projective Simson line". The Mathematical Gazette (99): 339-341. doi:10.1017/mag.2015.47. 6 Mart 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020. 
9. ^ Dao, O.T (29 Temmuz 2013). "Two Pascals merge into one". Cut-the-Knot. 26 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020. 

• Ayme, Jean-Louis (2004), A Purely Synthetic Proof of the Droz-Farny Line Theorem (PDF), 4, Forum Geometricorum, ss. 219-224, 31 Aralık 2019 tarihinde kaynağından arşivlendi (PDF), erişim tarihi: 23 Ekim 2020  veya Alternatif Bağlantı (PDF), 15 Şubat 2020 tarihinde kaynağından arşivlendi (PDF), erişim tarihi: 23 Ekim 2020 
• Thas, Charles (2006), A Note on the Droz-Farny Theorem, 6, Forum Geometricorum [electronic only] 
• Struve, R; Struve, H. (2016), "An axiomatic analysis of the Droz-Farny Line Theorem", Aequat. Math., 90, ss. 1201-1218, doi:10.1007/s00010-016-0430-2 

• "Droz-Farny Line Theorem" (Java Applet). cut-the-knot. 27 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020. 
• "A generalization of Droz-Farny line theorem". geogebra. 28 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020. 
• "Goormaghtigh's generalization of the Droz-Farny Line". geogebra. 26 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020. 
• "Droz-Farny line on a sphere". geogebra. 26 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Ekim 2020.