Centripetalna sila

Centripetalna sila (od latinskih reči centrum, „centar” i petere, „tražiti”[1]) je sila koja uzrokuje da telo sledi zakrivljenu putanju. Njen pravac je uvek ortogonalan na vektor brzine tela u datoj tački i usmeren je prema centru zakrivljenosti putanje.
Najjednostavniji slučaj delovanja centripetalne sile je kružno kretanje u kojem se telo kreće konstantnom brzinom po kružnici. Centripetalna sila je u ovom slučaju usmerena duž poluprečnika kruga od tačke u kojoj se telo u datom trenutku nalazi ka centru kruga.[2][3]
Matematički opis kretanja tela po kružnoj putanji izveo je holandski fizičar Kristijan Hajgens 1659. godine.[4] Isak Njutn je centripetalnu silu opisao kao „silu kojom se tela povlače ili prisiljavaju, ili na bilo koji način teže ka tački kao centru”.[5] U Njutnovoj mehanici, sila gravitacija je centripetalna sila koja je odgovorna za orbitalna kretanja planeta, satelita, itd.

Pojam centrifugalne sile se objašnjava preko centripetalne sile. Centripetalna sila je realna sila koja deluje na telo pri kružnom kretanju gledano iz stacionarnog inercijalnog sistema referencije. U pokretnom neinercijalnom sistemu referencije vezanom za telo koje rotira, ne vidi se centripetalna sila, ali da bi se objasnilo kretanje tela uvodi se centrifugalna sila koja ima isti intenzitet i pravac kao centripetalna sila, ali je suprotnog smera u odnosu na centripetalnu silu i usmerena je od centra zakrivljene putanje ka telu.
Formula
Centripetalna sila koja deluje na objekt mase m koji se kreće po kružnici je zadata Drugim Njutnovim zakonom:
gde je centripetalno ubrzanje koje se za telo koje se kreće tangencijalnom brzinom v duž puta radijusa zakrivljenosti r može izračunati kao:[6]
tako da za centripetalnu silu važi:
gde je razlika između vektora brzine. Pošto vektori brzine u gornjem dijagramu imaju konstantnu veličinu i pošto je svaki okomit na svoj odgovarajući vektor položaja, jednostavno oduzimanje vektora podrazumeva dva slična jednakokraka trougla sa kongruentnim uglovima – jedan koji sadrži osnovu od i dužinu noge od , a drugi osnovu od (razlika u vektoru položaja) i dužina noge od :[7]
Stoga, može se zameniti sa :[7]
pravac sile je ka centru kružnice u kojoj se objekat kreće, odnosno oskulirajućim krugom (krug koji najbolje odgovara lokalnoj putu, ako putanja nije kružna).[8] Brzina u formuli je na kvadrat, tako da je za dvostruku brzinu potrebna četiri puta veća sila. Inverzni odnos sa radijusom krivine pokazuje da je za pola radijalnog rasta potrebna dvostruko veća sila.
Centripetalna sila izražena preko ugaonih veličina
Centripetalna sila se ponekad izražava preko ugaone brzine objekta ω koji rotira oko centra kruga. Ugaona brzina je vezana za tangencijalnu brzinu formulom
tako da je centripetalna sila preko ugaone brzine izražena kao:
Centripetalna sila se za periodična kretanja može izraziti i preko perioda T , odnosno vremena potrebnom da telo napravi pun obrt oko centra kruga. Kako je veza između ugaone brzine i perioda , jednačina za centripetalnu silu postaje:
- [9]
Centripetalna sila kod relativističkog kretanja
U akceleratorima čestica, brzina čestica može biti veoma visoka (uporediva sa brzinom svetlosti u vakuumu). Za kretanje kod tako velikih relativističkih brzina ne važi klasična mehanika, već se mora koristiti fizika specijalne relativnosti.
Izraz za centripetalnu silu pri relativističkom kretanju je:[10]
gde je
Lorencov faktor.[11][12]
Izvori

U slučaju predmeta koji se ljulja oko kraja užeta u horizontalnoj ravni, centripetalna sila na predmet se obezbeđuje zatezanjem užeta. Primer užeta je primer koji uključuje silu 'povlačenja'. Centripetalna sila se takođe može isporučiti kao sila 'guranja', kao na primer u slučaju kada normalna reakcija zida obezbeđuje centripetalnu silu za zid smrti ili vozača rotora.
Njutnova ideja o centripetalnoj sili odgovara onome što se danas naziva centralnom silom. Kada je satelit u orbiti oko planete, gravitacija se smatra centripetalnom silom iako je u slučaju ekscentričnih orbita gravitaciona sila usmerena ka fokusu, a ne prema trenutnom centru zakrivljenosti.[14]
Drugi primer centripetalne sile nastaje u spirali koja se nalazi kada se naelektrisana čestica kreće u uniformnom magnetnom polju u odsustvu drugih spoljnih sila. U ovom slučaju, magnetna sila je centripetalna sila koja deluje prema osi spirale.
Primeri
Za telo koje pomoću užeta rotira u horizontalnoj ravni, u ulozi centripetalne sile koja izaziva kružno kretanje tela je sila zatezanja užeta. U ovom slučaju centripetalna sila je sila povlačenja. Centripetalna sila može biti pružena i kao sila guranja, kao u slučaju kada normalna reakcija zida pruža centripetalnu silu vozaču na zidu smrti.
Kada naelektrisana čestica uđe u uniformno magnetno polje pod pravim uglom u odnosu na pravac polja, magnetna sila će biti centripetalna sila za naelektrisanu česticu i u odsustvu drugih spoljašnjih sila, čestica će se kretati po spirali oko magnetnog polja. Kada naelektrisana čestica izgubi svoju brzinu, kretaće se po kružnici oko ose magnetnog polja.
Analiza nekoliko slučajeva
Ispod su data tri primera sve veće složenosti, sa izvođenjem formula za brzinu i ubrzanje.
Ujednačeno kružno kretanje
Ravnomerno kružno kretanje se odnosi na slučaj konstantne brzine rotacije. Slede dva pristupa opisa ovog slučaja.
Računsko izvođenje
U dve dimenzije, vektor položaja , koji ima veličinu (dužinu) i usmeren pod uglom iznad x-ose, može se izraziti u Dekartovim koordinatama pomoću jediničnih vektora and :[15]
Pretpostavka o ravnomernom kružnom kretanju zahteva tri uslova:
- Objekat se kreće samo po krugu.
- Poluprečnik kruga se ne menja tokom vremena.
- Objekat se kreće konstantnom ugaonom brzinom oko kruga. Prema tome, gde je vreme.
Brzina kretanja i ubrzanje su prvi i drugi derivati položaja u odnosu na vreme:
Termin u zagradi je originalni izraz u Dekartovim koordinatama. Sledstveno, negativna vrednost pokazuje da je ubrzanje usmereno ka centru kruga (nasuprot poluprečnika), te se zato naziva „centripetalno” (tj. „tražeći centar”). Dok objekti prirodno prate pravu putanju (zbog inercije), ovo centripetalno ubrzanje opisuje kružnu putanju kretanja uzrokovanu centripetalnom silom.
Izvođenje pomoću vektora

Slika desno prikazuje vektorske odnose za ravnomerno kružno kretanje. Sama rotacija je predstavljena vektorom ugaone brzine Ω, koji je normalan na ravan orbite (pomoću pravila desne ruke) i ima veličinu datu kao:
sa θ ugaonim položajem u trenutku t. U ovom pododeljku, dθ/dt se pretpostavlja da je konstantno, nezavisno od vremena. Pređeno rastojanje dℓ čestice za vreme dt duž kružne putanje je
koje po svojstvima vektorskog unakrsnog proizvoda ima magnitudu rdθ i nalazi se u pravcu tangente na kružnu putanju.
Shodno tome,
Drugim rečima,
Diferencirajući u odnosu na vreme,
Lagranžova formula navodi:
Primenjujući Lagranžovu formulu uz zapažanje da je Ω • r(t) = 0 u svakom trenutku,
Rečju, ubrzanje je usmereno direktno suprotno od radijalnog pomeranja r u svakom trenutku i ima magnitudu:
gde vertikalne šipke |...| označavaju vektorsku veličinu, koja je u slučaju r(t) jednostavno poluprečnik r putanje. Ovaj rezultat se slaže sa prethodnim odeljkom, iako je notacija malo drugačija.
Kada se brzina rotacije učini konstantnom u analizi neujednačenog kružnog kretanja, ta analiza se slaže sa ovom.
Prednost vektorskog pristupa je u tome što je očigledno nezavisan od bilo kog koordinatnog sistema.
Primer: Nagnuto skretanje

Gornji panel na slici desno prikazuje loptu u kružnom kretanju na nagnutoj krivini. Kriva je nagnuta pod uglom θ u odnosu na horizontalu, a površina puta se smatra klizavom. Cilj je pronaći koji ugao mora imati bankina da lopta ne sklizne sa puta.[16] Intuicija nam govori da će, na ravnoj krivini bez ikakvog nagiba, lopta jednostavno skliznuti sa puta; dok sa veoma strmim nagibom, lopta će kliziti do centra osim ako brzo putuje krivinom.
Osim bilo kakvog ubrzanja koje se može dogoditi u pravcu putanje, donji panel gornje slike pokazuje sile na loptu. Postoje dve sile; jedna je sila gravitacije vertikalno nadole kroz centar mase lopte mg, gde je m masa lopte, a g gravitaciono ubrzanje; druga je normalna sila naviše koju vrši put pod pravim uglom u odnosu na površinu puta man. Centripetalna sila koju zahteva zakrivljeno kretanje je takođe prikazana iznad. Ova centripetalna sila nije treća sila primenjena na loptu, već se mora obezbediti neto silom na loptu koja je rezultat vektorskog sabiranja normalne sile i sile gravitacije. Rezultantna ili neto sila na lopti pronađena vektorskim sabiranjem normalne sile koju vrši put i vertikalne sile usled gravitacije mora biti jednaka centripetalnoj sili koju diktira potreba da se putuje kružnom putanjom. Zakrivljeno kretanje se održava sve dok ova neto sila obezbeđuje centripetalnu silu potrebnu za kretanje.
Horizontalna neto sila na loptu je horizontalna komponenta sile od puta, koja ima magnitudu |Fh| = m|an| sin θ. Vertikalna komponenta sile od puta mora da se suprotstavi gravitacionoj sili: |Fv| = m|an| cos θ = m|g|, što implicira |an| = |g| / cos θ. Zamena u gornju formulu za |Fh| daje horizontalnu silu koja je:
S druge strane, pri brzini |v| na kružnoj putanji poluprečnika r, kinematika kaže da je sila potrebna da se lopta neprekidno okreće u zaokretu radijalno unutra centripetalna sila Fc magnitude:
Sledstveno, lopta je na stabilnoj putanji kada je ugao puta postavljen tako da se zadovolji uslov: ili,
Kako se ugao nagiba θ približava 90°, tangentna funkcija se približava beskonačnosti, dozvoljavajući veće vrednosti za |v|2/r. Ova jednačina navodi da za veće brzine (veće |v|) put mora biti strmije nagnut (veća vrednost za θ), a za oštrija skretanja (manje r) put takođe mora biti strmije nagnut, što je u skladu sa intuicijom. Kada ugao θ ne zadovoljava gornji uslov, horizontalna komponenta sile koju vrši put ne obezbeđuje ispravnu centripetalnu silu, a dodatna sila trenja tangencijalna na površinu puta se poziva da obezbedi razliku. Ako trenje to ne može da uradi (tj. koeficijent trenja je prekoračen), lopta klizi na drugi radijus gde se ravnoteža može ostvariti.[17][18]
Ove ideje važe i za vazdušni let. Pogledajte uputstvo za FAA pilote.[19]
Neujednačeno kružno kretanje

Kao generalizacija slučaja ravnomernog kružnog kretanja, pretpostavimo da ugaona brzina rotacije nije konstantna. Ubrzanje sada ima tangencijalnu komponentu, kao što je prikazano na slici desno. Ovaj slučaj se koristi za demonstriranje strategije derivacije zasnovane na polarnom koordinatnom sistemu.
Neka je r(t) vektor koji opisuje položaj tačke mase kao funkciju vremena. Pošto se pretpostavlja kružno kretanje, neka je r(t) = R·ur, gde je R konstanta (poluprečnik kruga), a ur je jedinični vektor koji ide od koordinatnog početka do tačke mase. Pravac ur je opisan sa θ, uglom između x-ose i jediničnog vektora, mereno u smeru suprotnom od kazaljke na satu od x-ose. Drugi jedinični vektor za polarne koordinate, uθ je okomit na ur i usmeren je u pravcu povećanja θ. Ovi polarni jedinični vektori mogu se izraziti u vidu Dekartovih jediničnih vektora u x i y pravcima, označeni kao i , respektivno:[20] and
Može se diferencirati da bi se pronašla brzina: gde je ω ugaona brzina dθ/dt.
Ovaj rezultat za brzinu odgovara očekivanjima da brzina treba da bude usmerena tangencijalno na krug i da veličina brzine treba da bude rω. Ponovnim diferenciranjem i konstatacijom da nalazi se da je ubrzanje a:
Dakle, radijalne i tangencijalne komponente ubrzanja su: and gde je |v| = r ω magnituda brzine.
Ove jednačine matematički izražavaju da se, u slučaju objekta koji se kreće duž kružne putanje sa promenljivom brzinom, ubrzanje tela može razložiti na okomitu komponentu koja menja smer kretanja (centripetalno ubrzanje) i paralelu, ili tangencijalna komponenta, koja menja brzinu.
Generalno planarno kretanje



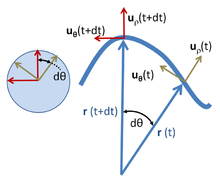
Polarne koordinate
Gore navedeni rezultati mogu se možda jednostavnije izvesti u polarnim koordinatama, i istovremeno proširiti na opšte kretanje unutar ravni, kao što je prikazano u nastavku. Polarne koordinate u ravni koriste radijalni jedinični vektor uρ i ugaoni jedinični vektor uθ, kao što je prikazano iznad.[21] Čestica na poziciji r je opisana sa:
gde se oznaka ρ koristi da opiše rastojanje putanje od koordinatnog početka umesto R da bi se naglasilo da ovo rastojanje nije fiksno, već da varira sa vremenom. Jedinični vektor uρ putuje sa česticom i uvek je usmeren u istom pravcu kao r(t). Jedinični vektor uθ takođe putuje sa česticom i ostaje ortogonalan na uρ. Dakle, uρ i uθ formiraju lokalni Dekartov koordinatni sistem vezan za česticu i vezan za putanju koju je prešla čestica.[22] Pomeranjem jediničnih vektora tako da im se repovi poklapaju, kao što se vidi u krugu levo na slici iznad, vidi se da uρ i uθ formiraju par pod pravim uglom sa vrhovima na jediničnom krugu koji se kreću napred-nazad po obodu ovog kruga sa istim uglom θ(t) kao r(t).
Kada se čestica kreće, njena brzina je
Za procenu brzine potreban je izvod jediničnog vektora uρ. Pošto je uρ jedinični vektor, njegova veličina je fiksna i može se menjati samo u pravac, odnosno njegova promena duρ ima komponentu samo upravnu na uρ. Kada trajektorija r(t) rotira za iznos dθ, uρ, koji je usmeren u istom pravcu kao i r(t), on takođe rotira za dθ. Vidi sliku iznad. Prema tome, promena uρ je
ili
Na sličan način je pronalazi brzina promene uθ. Kao i kod uρ, uθ je jedinični vektor i može samo da se rotira bez promene veličine. Da ostane ortogonalan na uρ dok trajektorija r(t) rotira za iznos dθ, uθ, koji je ortogonalan na r(t), takođe rotira za dθ. Vidi sliku iznad. Prema tome, promena duθ je ortogonalna na uθ i proporcionalna sa dθ (pogledajte sliku iznad):
Jednačina iznad pokazuje da je predznak negativan: da bi se održala ortogonalnost, ako je duρ pozitivan sa dθ, onda duθ mora da se smanji.
Zamena derivata uρ u izraz za brzinu:
Da bi se dobilo ubrzanje, vrši se još jedno vremenska diferencijacija:
Zamenom derivata od uρ i uθ, ubrzanje čestice je:[23]
Kao poseban primer, ako se čestica kreće u krugu konstantnog radijusa R, onda je dρ/dt = 0, v = vθ, i:
gde je
Ovi rezultati se slažu sa onima iznad za neujednačeno kružno kretanje. Pogledajte i članak o neujednačenom kružnom kretanju. Ako se ovo ubrzanje pomnoži sa masom čestice, vodeći član je centripetalna sila, a negativna vrednost drugog člana koji se odnosi na ugaono ubrzanje se ponekad naziva Ojlerova sila.[24]
Za putanje koje nisu kružno kretanje, na primer, opštiju putanju prikazanu na gornjoj slici, trenutni centar rotacije i poluprečnik krivine putanje su povezani samo indirektno sa koordinatnim sistemom definisanim sa uρ i uθ i sa dužinom |r(t)| = ρ. Shodno tome, u opštem slučaju, nije jednostavno odvojiti centripetalne i Ojlerove članove iz gornje opšte jednačine ubrzanja.[25][26] Da bi se direktno adresiralo ovo pitanje, poželjnije su lokalne koordinate, kao što će biti reči u nastavku.
Lokalne koordinate
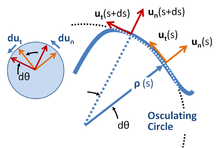
Lokalne koordinate označavaju skup koordinata koje putuju sa česticom,[27] i imaju orijentaciju koja je određena putanjom čestice.[28] Jedinični vektori se formiraju kao što je prikazano na slici desno, oba, tangencijalni i normalni na putanju. Ovaj koordinatni sistem se ponekad naziva unutrašnjim koordinatama ili koordinatama putanje[29][30] ili nt-koordinatama, za normalno-tangencijalno, koje se odnose na ove jedinične vektore. Ove koordinate su veoma poseban primer opštijeg koncepta lokalnih koordinata iz teorije diferencijalnih oblika.[31]
Rastojanje duž putanje čestice je dužina luka s, za koju se smatra da je poznata funkcija vremena.
Centar zakrivljenosti je definisan na svakoj poziciji s koja se nalazi na rastojanju ρ (poluprečnik krivine) od krive na liniji duž normale un (s). Zahtevano rastojanje ρ(s) na dužini luka s je definisano u smislu brzine rotacije tangente na krivu, koja je zauzvrat određena samom putanjom. Ako je orijentacija tangente u odnosu na neku početnu poziciju θ(s), onda je ρ(s) definisano izvodom dθ/ds:
Poluprečnik krive se obično uzima da je pozitivan (odnosno kao apsolutna vrednost), dok je zakrivljenost κ veličina sa predznakom.
Geometrijski pristup pronalaženju centra krivine i poluprečnika krivine koristi ograničavajući proces koji vodi do oskulacionog kruga.[32][33] Vidi sliku iznad.
Koristeći ove koordinate, kretanje duž putanje se posmatra kao niz kružnih putanja stalno promenljivog centra, i na svakoj poziciji s predstavlja neujednačeno kružno kretanje na toj poziciji poluprečnika ρ. Lokalna vrednost ugaone brzine rotacije je tada data sa:
sa lokalnom brzinom v datom sa:
Što se tiče ostalih primera iznad, pošto jedinični vektori ne mogu da menjaju veličinu, njihova brzina promene je uvek okomita na njihov pravac (pogledajte levi umetak na slici iznad):[34]
Prema tome, brzina i ubrzanje su:[33][35][36]
i koristeći lančano pravilo diferencijacije:
- with the tangential acceleration
U ovom lokalnom koordinatnom sistemu, ubrzanje liči na izraz za neujednačeno kružno kretanje sa lokalnim radijusom ρ(s), a centripetalno ubrzanje je identifikovano kao drugi član.[37]
Proširivanje ovog pristupa na trodimenzionalne prostorne krive dovodi do Frenet-Seretovih formula.[38][39]
Alternativni pristup
Gledajući gornju sliku, neko bi se mogao zapitati da li je uzeta u obzir razlika u krivini između ρ(s) i ρ(s + ds) pri izračunavanju dužine luka kao ds = ρ(s)dθ. Uverenje po ovom pitanju može se naći korišćenjem formalnijeg pristupa koji je naveden u nastavku. Ovaj pristup uspostavlja vezu i sa člankom o zakrivljenosti.
Da bi se uveli jedinični vektori lokalnog koordinatnog sistema, jedan pristup je da se počne od Dekartovih koordinata i opišu lokalne koordinate u smislu ovih Dekartovih koordinata. U pogledu dužine luka s, neka putanja bude opisana kao:[40]
Tada se inkrementalno pomeranje duž putanje ds opisuje sa:
gde se uvode prosti brojevi za označavanje izvoda u odnosu na s. Veličina ovog pomaka je ds, što pokazuje da:[41]
- (Eq. 1)
Ovo pomeranje je nužno tangenta na krivu u s, pokazujući da je jedinični vektor tangenta na krivu:
dok je spoljašnji jedinični vektor normalan na krivu
Ortogonalnost se može proveriti pokazujući da je skalarni proizvod vektor nula. Jedinična veličina ovih vektora je posledica jednačine 1. Koristeći vektor tangente, ugao θ tangente na krivu je dat sa:
and
Poluprečnik krivine se uvodi potpuno formalno (bez potrebe za geometrijskom interpretacijom) kao:
Izvod na θ se može naći iz onog za sinθ:
Sada:
u kome je imenilac jedinica. Sa ovom formulom za izvod sinusa, poluprečnik krivine postaje:
gde ekvivalencija oblika proizilazi iz diferencijacije jednačine 1:
Sa ovim rezultatima, ubrzanje se može naći da je:
što se može proveriti uzimanjem skalarnog proizvoda sa jediničnim vektorima ut(s) i un(s). Ovaj rezultat za ubrzanje je isti kao i za kružno kretanje zasnovano na poluprečniku ρ. Koristeći ovaj koordinatni sistem u inercijalnom okviru, lako je identifikovati silu koja je normalna na putanju kao centripetalnu silu, a onu paralelnu sa putanjom kao tangencijalnu silu. Sa kvalitativnog stanovišta, putanja se može aproksimirati lukom kružnice za ograničeno vreme, i za ograničeno vreme se primenjuje određeni radijus krivine, te se centrifugalne i Ojlerove sile mogu analizirati na osnovu kružnog kretanja sa tim poluprečnikom.
Ovaj rezultat za ubrzanje se slaže sa onim ranije pronađenim. Međutim, u ovom pristupu, pitanje promene poluprečnika zakrivljenosti sa s se rešava potpuno formalno, u skladu sa geometrijskom interpretacijom, ali ne oslanjajući se na nju, čime se izbegavaju bilo kakva pitanja koja bi gornja slika mogla da sugeriše o zanemarivanju varijacije u ρ.
Primer: kružno kretanje
Da bismo ilustrovali gornje formule, neka su x, y dati kao:
Onda je:
koje se može prepoznati kao kružna putanja oko koordinatnog početka sa poluprečnikom α. Položaj s = 0 odgovara [α, 0] ili 3 sata. Da bi se koristio gornji formalizam, potrebni su derivati:
Sa ovim rezultatima, može se potvrditi da:
Jedinični vektori se takođe mogu naći:
koji služe da se pokaže da se s = 0 nalazi na poziciji [ρ, 0] i s = ρπ/2 at [0, ρ], što se slaže sa originalnim izrazima za x i y. Drugim rečima, s se meri u suprotnom smeru od kazaljke na satu oko kruga od 3 sata. Takođe, mogu se naći derivati ovih vektora:
Za dobijanje brzine i ubrzanja neophodna je vremenska zavisnost za s. Za kretanje suprotno od kazaljke na satu pri promenljivoj brzini v(t):
gde je v(t) brzina i t vreme, i s(t = 0) = 0. Onda je:
gde je već utvrđeno da je α = ρ. Ovo ubrzanje je standardni rezultat za neujednačeno kružno kretanje.
Vidi još
Reference
- ^ Craig, John (1849). A new universal etymological, technological and pronouncing dictionary of the English language: embracing all terms used in art, science, and literature, Volume 1. Harvard University. стр. 291. Extract of page 291
- ^ Russelkl C Hibbeler (2009). „Equations of Motion: Normal and tangential coordinates”. Engineering Mechanics: Dynamics (12 изд.). Prentice Hall. стр. 131. ISBN 978-0-13-607791-6.
- ^ Paul Allen Tipler; Gene Mosca (2003). Physics for scientists and engineers (5th изд.). Macmillan. стр. 129. ISBN 978-0-7167-8339-8.
- ^ P. Germain; M. Piau; D. Caillerie, ур. (2012). Theoretical and Applied Mechanics. Elsevier. ISBN 9780444600202.
- ^ Newton, Isaac (2010). The principia : mathematical principles of natural philosophy. [S.l.]: Snowball Pub. стр. 10. ISBN 978-1-60796-240-3.
- ^ Chris Carter (2001). Facts and Practice for A-Level: Physics. S.2.: Oxford University Press. стр. 30. ISBN 978-0-19-914768-7.
- ^ а б OpenStax CNX. „Uniform Circular Motion”.
- ^ Eugene Lommel; George William Myers (1900). Experimental physics. K. Paul, Trench, Trübner & Co. стр. 63.
- ^ Colwell, Catharine H. „A Derivation of the Formulas for Centripetal Acceleration”. PhysicsLAB. Архивирано из оригинала 15. 08. 2011. г. Приступљено 31. 7. 2011.
- ^ Conte, Mario; Mackay, William W (1991). An Introduction to the Physics of Particle Accelerators. World Scientific. стр. 8. ISBN 978-981-4518-00-0. Extract of page 8
- ^ Forshaw, Jeffrey; Smith, Gavin (2014). Dynamics and Relativity. John Wiley & Sons. ISBN 978-1-118-93329-9.
- ^ One universe, by Neil deGrasse Tyson, Charles Tsun-Chu Liu, and Robert Irion.
- ^ Knudsen, Jens M.; Hjorth, Poul G. (2000). Elements of Newtonian mechanics: including nonlinear dynamics (3 изд.). Springer. стр. 96. ISBN 3-540-67652-X.
- ^ Theo Koupelis (2010). In Quest of the Universe (6th изд.). Jones & Bartlett Learning. стр. 83. ISBN 978-0-7637-6858-4.
- ^ A. V. Durrant (1996). Vectors in physics and engineering. CRC Press. стр. 103. ISBN 978-0-412-62710-1.
- ^ Lawrence S. Lerner (1997). Physics for Scientists and Engineers. Boston: Jones & Bartlett Publishers. стр. 128. ISBN 978-0-86720-479-7.
- ^ Arthur Beiser (2004). Schaum's Outline of Applied Physics. New York: McGraw-Hill Professional. стр. 103. ISBN 978-0-07-142611-4.
- ^ Alan Darbyshire (2003). Mechanical Engineering: BTEC National Option Units. Oxford: Newnes. стр. 56. ISBN 978-0-7506-5761-7.
- ^ Federal Aviation Administration (2007). Pilot's Encyclopedia of Aeronautical Knowledge. Oklahoma City OK: Skyhorse Publishing Inc. Figure 3–21. ISBN 978-1-60239-034-8.
- ^ Note: unlike the Cartesian unit vectors and , which are constant, in polar coordinates the direction of the unit vectors ur and uθ depend on θ, and so in general have non-zero time derivatives.
- ^ Although the polar coordinate system moves with the particle, the observer does not. The description of the particle motion remains a description from the stationary observer's point of view.
- ^ Notice that this local coordinate system is not autonomous; for example, its rotation in time is dictated by the trajectory traced by the particle. The radial vector r(t) does not represent the radius of curvature of the path.
- ^ John Robert Taylor (2005). Classical Mechanics. Sausalito CA: University Science Books. стр. 28—29. ISBN 978-1-891389-22-1.
- ^ Cornelius Lanczos (1986). The Variational Principles of Mechanics. New York: Courier Dover Publications. стр. 103. ISBN 978-0-486-65067-8.
- ^ See, for example, Howard D. Curtis (2005). Orbital Mechanics for Engineering Students. Butterworth-Heinemann. стр. 5. ISBN 978-0-7506-6169-0.
- ^ S. Y. Lee (2004). Accelerator physics (2nd изд.). Hackensack NJ: World Scientific. стр. 37. ISBN 978-981-256-182-4.
- ^ The observer of the motion along the curve is using these local coordinates to describe the motion from the observer's frame of reference, that is, from a stationary point of view. In other words, although the local coordinate system moves with the particle, the observer does not. A change in coordinate system used by the observer is only a change in their description of observations, and does not mean that the observer has changed their state of motion, and vice versa.
- ^ Zhilin Li; Kazufumi Ito (2006). The immersed interface method: numerical solutions of PDEs involving interfaces and irregular domains. Philadelphia: Society for Industrial and Applied Mathematics. стр. 16. ISBN 978-0-89871-609-2.
- ^ K L Kumar (2003). Engineering Mechanics. New Delhi: Tata McGraw-Hill. стр. 339. ISBN 978-0-07-049473-2.
- ^ Lakshmana C. Rao; J. Lakshminarasimhan; Raju Sethuraman; SM Sivakuma (2004). Engineering Dynamics: Statics and Dynamics. Prentice Hall of India. стр. 133. ISBN 978-81-203-2189-2.
- ^ Shigeyuki Morita (2001). Geometry of Differential Forms
 . American Mathematical Society. стр. 1. ISBN 978-0-8218-1045-3. „local coordinates.”
. American Mathematical Society. стр. 1. ISBN 978-0-8218-1045-3. „local coordinates.” - ^ The osculating circle at a given point P on a curve is the limiting circle of a sequence of circles that pass through P and two other points on the curve, Q and R, on either side of P, as Q and R approach P. See the online text by Lamb: Horace Lamb (1897). An Elementary Course of Infinitesimal Calculus. University Press. стр. 406. ISBN 978-1-108-00534-0. „osculating circle.”
- ^ а б Guang Chen; Fook Fah Yap (2003). An Introduction to Planar Dynamics (3rd изд.). Central Learning Asia/Thomson Learning Asia. стр. 34. ISBN 978-981-243-568-2.
- ^ R. Douglas Gregory (2006). Classical Mechanics: An Undergraduate Text. Cambridge University Press. стр. 20. ISBN 978-0-521-82678-5.
- ^ Edmund Taylor Whittaker; William McCrea (1988). A Treatise on the Analytical Dynamics of Particles and Rigid Bodies: with an introduction to the problem of three bodies (4th изд.). Cambridge University Press. стр. 20. ISBN 978-0-521-35883-5.
- ^ Jerry H. Ginsberg (2007). Engineering Dynamics. Cambridge University Press. стр. 33. ISBN 978-0-521-88303-0.
- ^ Joseph F. Shelley (1990). 800 solved problems in vector mechanics for engineers: Dynamics. McGraw-Hill Professional. стр. 47. ISBN 978-0-07-056687-3.
- ^ Larry C. Andrews; Ronald L. Phillips (2003). Mathematical Techniques for Engineers and Scientists. SPIE Press. стр. 164. ISBN 978-0-8194-4506-3.
- ^ Ch V Ramana Murthy; NC Srinivas (2001). Applied Mathematics. New Delhi: S. Chand & Co. стр. 337. ISBN 978-81-219-2082-7.
- ^ The article on curvature treats a more general case where the curve is parametrized by an arbitrary variable (denoted t), rather than by the arc length s.
- ^ Ahmed A. Shabana; Khaled E. Zaazaa; Hiroyuki Sugiyama (2007). Railroad Vehicle Dynamics: A Computational Approach. CRC Press. стр. 91. ISBN 978-1-4200-4581-9.
Literatura
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th изд.). Brooks/Cole. ISBN 978-0-534-40842-8.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th изд.). W. H. Freeman. ISBN 978-0-7167-0809-4.
- Centripetal force vs. Centrifugal force, from an online Regents Exam physics tutorial by the Oswego City School District
- Lanczos, Cornelius (1970). The variational principles of mechanics (4th изд.). New York: Dover Publications Inc. Introduction, pp. xxi–xxix. ISBN 0-486-65067-7.
- Synge, J. L. (1960). „Classical dynamics”. Ур.: Flügge, S. Principles of Classical Mechanics and Field Theory / Prinzipien der Klassischen Mechanik und Feldtheorie. Encyclopedia of Physics / Handbuch der Physik. 2 / 3 / 1. Berlin, Heidelberg: Springer Berlin Heidelberg. ISBN 978-3-540-02547-4. OCLC 165699220. doi:10.1007/978-3-642-45943-6.
- Arnolʹd, VI (1989). Mathematical methods of classical mechanics (2nd изд.). Springer. Chapter 8. ISBN 978-0-387-96890-2.
- Doran, C; Lasenby, A (2003). Geometric algebra for physicists. Cambridge University Press. стр. §12.3, pp. 432–439. ISBN 978-0-521-71595-9.
- Merrifield, Michael. „γ – Lorentz Factor (and time dilation)”. Sixty Symbols. Brady Haran for the University of Nottingham.
- Merrifield, Michael. „γ2 – Gamma Reloaded”. Sixty Symbols. Brady Haran for the University of Nottingham.
- Gomez, R W; Hernandez-Gomez, J J; Marquina, V (25. 7. 2012). „A jumping cylinder on an inclined plane”. Eur. J. Phys. IOP. 33 (5): 1359—1365. Bibcode:2012EJPh...33.1359G. S2CID 55442794. arXiv:1204.0600
 . doi:10.1088/0143-0807/33/5/1359. Приступљено 25. 4. 2016. CS1 одржавање: Формат датума (веза)
. doi:10.1088/0143-0807/33/5/1359. Приступљено 25. 4. 2016. CS1 одржавање: Формат датума (веза)
Spoljašnje veze

- Notes from University of Winnipeg
- Notes from Physics and Astronomy HyperPhysics at Georgia State University; see also home page
- Notes from Britannica
- Notes from PhysicsNet
- NASA notes by David P. Stern
- Notes from U Texas.
- Analysis of smart yo-yo
- The Inuit yo-yo
- Kinematic Models for Design Digital Library (KMODDL)






































![{\displaystyle \mathbf {a} \ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathrm {d} \mathbf {v} }{d\mathrm {t} }}=\mathbf {\Omega } \times {\frac {\mathrm {d} \mathbf {r} (t)}{\mathrm {d} t}}=\mathbf {\Omega } \times \left[\mathbf {\Omega } \times \mathbf {r} (t)\right]\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bdc59db211dba1e224034884d244146c97c2ba)























![{\displaystyle {\begin{aligned}\mathbf {a} &={\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}\mathbf {u} _{\rho }+2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}-\rho \mathbf {u} _{\rho }\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\ ,\\&=\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]\\&=\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} v_{\rho }}{\mathrm {d} t}}-{\frac {v_{\theta }^{2}}{\rho }}\right]+\mathbf {u} _{\theta }\left[{\frac {2}{\rho }}v_{\rho }v_{\theta }+\rho {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {v_{\theta }}{\rho }}\right]\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bd23fad91b9a145bc62e918b5124ee62c4a537b)
![{\displaystyle \mathbf {a} =\mathbf {u} _{\rho }\left[-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]=\mathbf {u} _{\rho }\left[-{\frac {v^{2}}{r}}\right]+\mathbf {u} _{\theta }\left[{\frac {\mathrm {d} v}{\mathrm {d} t}}\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/df2f314be17d32d8d204bef757376219863181c7)










![{\displaystyle \mathbf {r} (s)=\left[x(s),\ y(s)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea9cb4aedaa6696cd195a0329b20a3a6d4c1f0d0)
![{\displaystyle \mathrm {d} \mathbf {r} (s)=\left[\mathrm {d} x(s),\ \mathrm {d} y(s)\right]=\left[x'(s),\ y'(s)\right]\mathrm {d} s\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e41305b24920b77bceb3d266edba4ab08249618)
![{\displaystyle \left[x'(s)^{2}+y'(s)^{2}\right]=1\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50c42e82eda34ce15d98149c930dfb7ba7cec77d)
![{\displaystyle \mathbf {u} _{\mathrm {t} }(s)=\left[x'(s),\ y'(s)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52a7fe41893b23da5d10fa21095cbf823374b339)
![{\displaystyle \mathbf {u} _{\mathrm {n} }(s)=\left[y'(s),\ -x'(s)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aefd42926b0e6c5fd1cdd0b91ae514b65fd3dfc0)







![{\displaystyle {\begin{aligned}\mathbf {a} (s)&={\frac {\mathrm {d} }{\mathrm {d} t}}\mathbf {v} (s)={\frac {\mathrm {d} }{\mathrm {d} t}}\left[{\frac {\mathrm {d} s}{\mathrm {d} t}}\left(x'(s),\ y'(s)\right)\right]\\&=\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)+\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}\left(x''(s),\ y''(s)\right)\\&=\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)-\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}{\frac {1}{\rho }}\mathbf {u} _{\mathrm {n} }(s)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5b63aca630aacb31a8ef0fc21bcf2f8e86af3ca)





![{\displaystyle \mathbf {u} _{\mathrm {t} }(s)=\left[-\sin {\frac {s}{\alpha }}\ ,\ \cos {\frac {s}{\alpha }}\right]\ ;\ \mathbf {u} _{\mathrm {n} }(s)=\left[\cos {\frac {s}{\alpha }}\ ,\ \sin {\frac {s}{\alpha }}\right]\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72b1a6646bfe5026f496df581576f09251db1a9c)
![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {u} _{\mathrm {t} }(s)=-{\frac {1}{\alpha }}\left[\cos {\frac {s}{\alpha }}\ ,\ \sin {\frac {s}{\alpha }}\right]=-{\frac {1}{\alpha }}\mathbf {u} _{\mathrm {n} }(s)\ ;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d6d3efccbed76c27507654645897ccc0b587b08)
![{\displaystyle \ {\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {u} _{\mathrm {n} }(s)={\frac {1}{\alpha }}\left[-\sin {\frac {s}{\alpha }}\ ,\ \cos {\frac {s}{\alpha }}\right]={\frac {1}{\alpha }}\mathbf {u} _{\mathrm {t} }(s)\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29f755d9d1bb8f6f884a3bdc8ae8d1be5147674a)














 Centripetalna_sila
Centripetalna_sila