Testul liniei orizontale

Funcția trece testul
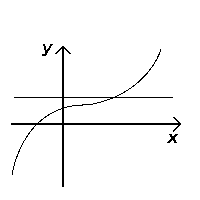
(este injectivă)

Funcția nu trece testul
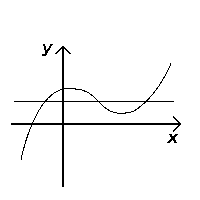
(nu este injectivă)

În matematică, testul liniei orizontale este utilizat pentru a determina dacă o funcție este injectivă.^[1]

O linie orizontală este o dreaptă paralelă cu axa absciselor. Având în vedere o funcție reală de variabilă reală ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} ,}$ se poate decide dacă este injectivă examinând cum intersectează dreptele orizontale graficul funcției. Dacă vreo linie orizontală ${\displaystyle y=c}$ intersectează graficul în mai multe puncte, funcția nu este injectivă. Pentru a constata acest lucru, trebuie observat că punctele de intersecție au aceeași valoare y (deoarece se află pe linia ${\displaystyle y=c}$) dar diferite valori x, ceea ce înseamnă prin definiție că funcția nu poate fi injectivă.^[1]

Variante ale testului liniei orizontale pot fi utilizate pentru a determina dacă o funcție este surjectivă sau bijectivă:

• Funcția f este surjectivă (adică, pe) dacă și numai dacă graficul său intersectează orice linie orizontală cel puțin o dată.
• Funcția f este bijectivă dacă și numai dacă graficul său intersectează orice linie orizontală o singură dată.

Fie funcția ${\displaystyle f\colon X\to Y}$ cu graficul său ca submulțime a produsului cartezian ${\displaystyle X\times Y}$. Fie liniile orizontale în ${\displaystyle X\times Y}$ :${\displaystyle \{(x,y_{0})\in X\times Y:y_{0}{\text{ este constant}}\}=X\times \{y_{0}\}}$. Funcția f este injectivă dacă și numai dacă fiecare linie orizontală intersectează graficul cel mult o dată. În acest caz, se spune că graficul trece testul liniei orizontale. Dacă vreo linie orizontală intersectează graficul de mai multe ori, funcția nu trece testul liniei orizontale și nu este injectivă.^[2]

• Funcție monotonă

Portal Matematică