Curva pedal

Para uma curva ${\displaystyle C}$ e um ponto fixado ${\displaystyle P,}$ a curva pedal de ${\displaystyle C}$ é o lugar geométrico dos pontos ${\displaystyle X}$ tais que ${\displaystyle PX}$ é perpendicular a tangente da curva que passa por ${\displaystyle X.}$ O ponto ${\displaystyle P}$ é chamado de ponto pedal. A curva pedal é a primeira de uma série de curvas ${\displaystyle C_{1},}$ ${\displaystyle C_{2},}$ ${\displaystyle C_{3},}$ etc.., onde ${\displaystyle C_{1}}$ é a curva pedal de ${\displaystyle C,}$ ${\displaystyle C_{2}}$ é a curva pedal de ${\displaystyle C_{1},}$ e assim por diante.

Mais precisamente, em qualquer ponto ${\displaystyle R}$ sobre ${\displaystyle C,}$ seja ${\displaystyle T}$ a reta tangente em ${\displaystyle R.}$ Existe um único ponto ${\displaystyle X}$ sobre ${\displaystyle T}$ que ou é ${\displaystyle P}$ (no caso de ${\displaystyle P}$ pertencer a ${\displaystyle T}$) ou forma com ${\displaystyle P}$ a reta perpendicular a ${\displaystyle T.}$ A curva pedal o conjunto dos tais pontos ${\displaystyle X,}$ chamados de pé da perpendicular a ${\displaystyle T}$ a partir de ${\displaystyle P,}$ conforme ${\displaystyle R}$ varia sobre pontos ${\displaystyle C.}$

Analogamente, existe um único ponto ${\displaystyle Y}$ sobre a reta normal à ${\displaystyle C}$ em ${\displaystyle R,}$ de forma que ${\displaystyle PY}$ seja perpendicular à normal, assim ${\displaystyle PXRY}$ é um retângulo (possivelmente degenerado). O lugar geométrico dos pontos ${\displaystyle Y}$ é chamado curva contrapedal.

Tome ${\displaystyle P}$ para ser a origem. Para obter uma curva dada pela equação ${\displaystyle F(x,y)=0,}$ se a equação da reta tangente em ${\displaystyle R=(x_{0},y_{0})}$ é escrita na forma

${\displaystyle \cos \alpha x+\mathrm {sen} \,\alpha y=p}$

em seguida o vetor (cos α, sin α) é paralelo ao segmento ${\displaystyle PX,}$ e o comprimento de ${\displaystyle PX,}$ que é a distância da partir reta tangente à origem, é ${\displaystyle p.}$ Também ${\displaystyle X}$ é representado em coordenadas polares por ${\displaystyle (p,\alpha )}$ e trocando ${\displaystyle (p,\alpha )}$ por ${\displaystyle (r,\theta )}$ produzimos a equação polar para a curva pedal.^[1]

Por exemplo,^[2] para a elipse

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$

a reta tangente em ${\displaystyle R=(x_{0},y_{0})}$ é

${\displaystyle {\frac {x_{0}x}{a^{2}}}+{\frac {y_{0}y}{b^{2}}}=1}$

e escrever isso na forma descrita acima requer que

${\displaystyle {\frac {x_{0}}{a^{2}}}={\frac {\cos \alpha }{p}},\,{\frac {y_{0}}{b^{2}}}={\frac {\mathrm {sen} \,\alpha }{p}}.}$

A equação para a elipse pode ser usada para eliminar ${\displaystyle x_{0}}$ and ${\displaystyle y_{0}}$ dando

${\displaystyle a^{2}\cos ^{2}\alpha +b^{2}\mathrm {sen} \,^{2}\alpha =p^{2},}$

e convertendo para ${\displaystyle (r,\theta )}$ dados

${\displaystyle a^{2}\cos ^{2}\theta +b^{2}\mathrm {sen} \,^{2}\theta =r^{2},}$

como a equação polar para a pedal. Isto é facilmente convertido para uma equação cartesiana

${\displaystyle a^{2}x^{2}+b^{2}y^{2}=(x^{2}+y^{2})^{2}.}$

Seja P a origem, e C dado em coordenadas polares pela equação r = f(θ). Seja R=(r, θ) um ponto na curva, e X=(p, α) seu ponto correspondente na curva polar. Façamos que ψ denote o ângulo entre a reta tangente e o raio vetor. Ele é dado por:

${\displaystyle r={\frac {dr}{d\theta }}\tan \psi .}$

Então

${\displaystyle p=r\sin \psi }$

e

${\displaystyle \alpha =\theta +\psi -{\frac {\pi }{2}}.}$

Essas equações podem ser usadas para produzir uma equação em p and α onde, quando transladado para r e θ, nos dá uma equação polar para a curva pedal. ^[3]

Por exemplo,^[4] seja a curva uma circunferência com r = a cos θ. Então

${\displaystyle a\cos \theta =-a\sin \theta \tan \psi }$

então

${\displaystyle \tan \psi =-\cot \theta ,\,\psi ={\frac {\pi }{2}}+\theta ,\alpha =2\theta .}$

Também temos

${\displaystyle p=r\sin \psi \ =r\cos \theta =a\cos ^{2}\theta =a\cos ^{2}{\alpha \over 2}.}$

Com isso a equação polar da pedal é:

${\displaystyle r=a\cos ^{2}{\theta \over 2}.}$

A equação Pedal de uma curva e seu pedal são muito relacionados. Se P é pego como o ponto pedal e como a origem, então pode ser mostrado que o ângulo ψ entre a curva e o raio vetor no ponto R é igual ao ângulo correspondente para a curva pedal no ponto X. Se p é o tamanho da perpendicular de P até a tangente a curva (i.e. PX) e q é o tamanho da correspondente perpendicular desenhada de P até a tangente ao pedal, então por semelhança de triângulos

${\displaystyle {\frac {p}{r}}={\frac {q}{p}}.}$

Disso segue imediatamente que se a equação Pedal da curva é f(p,r)=0 então a equação para a curva pedal é ^[5]

${\displaystyle f(r,{\frac {r^{2}}{p}})=0}$

Com isso, todos os pedais positivos e negativos podem ser computados facilmente se a equação pedal da curva é conhecida.

Seja ${\displaystyle {\vec {v}}=P-R}$ o vetor de R até P e sejam

${\displaystyle {\vec {v}}={\vec {v}}_{\parallel }+{\vec {v}}_{\perp }}$,

as componentes normal e tangencial de ${\displaystyle {\vec {v}}}$ com respeito a curva. Então ${\displaystyle {\vec {v}}_{\parallel }}$ é o vetor de R até X do qual a posição de X pode ser analisada.

Especificamente, se c é uma parametrização da curva então

${\displaystyle t\mapsto c(t)+{c'(t)\cdot (P-c(t)) \over |c'(t)|^{2}}c'(t)}$

parametriza a currva pedal (excetuando-se pontos onde c' é zero ou indefinido).

Para uma curva paramétrica definida, sua curva pedal com o ponto pedal (0,0) é definida como:

${\displaystyle X[x,y]={\frac {(xy'-yx')y'}{x'^{2}+y'^{2}}}}$

${\displaystyle Y[x,y]={\frac {(yx'-xy')x'}{x'^{2}+y'^{2}}}.}$

Considere um ângulo movendo-se rigidamente de forma que um de seus extremos seja fixo no ponto P, e o outro lado seja tangente a curva. Então, o vértice desse ângulo é X e traça assim, a curva pedal. Enquanto o ângulo se move, a direção do movimento em P é paralelo a PX a a direção do movimento em R é paralela a tangente T = RX. Portanto o centro instantâneo de rotação é a interseção da linha perpendicular a PX em P e perpendicular a RX em R, e esse ponto é Y. Assim, segue que a tangente à pedal em X é perpendicular a XY

Desenhe uma circunferência com diâmetro PR, então ela circunscreve o retângulo PXRY e XY é outro diâmetro. A circunferência e a pedal, são ambas perpendiculares a XY então elas são tangentes em X. Portanto a pedal é o envelope da circunferência com diâmetro PR onde R pertence à curva.

A linha YR é normal à curva e o envelope de tal normal e sua evoluta. Portanto YR é tangente a evoluta e o ponto Y é o pé da perpendicular de P a essa tangente, em outras palavras Y está no pedal da evoluta.

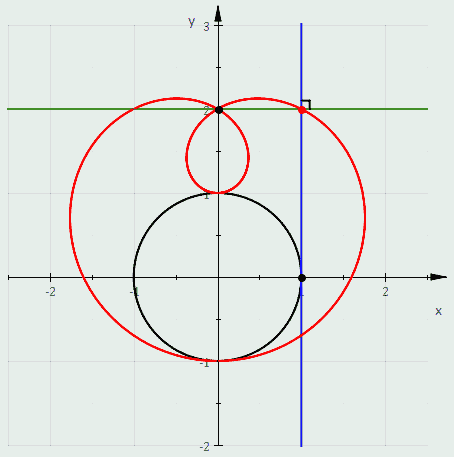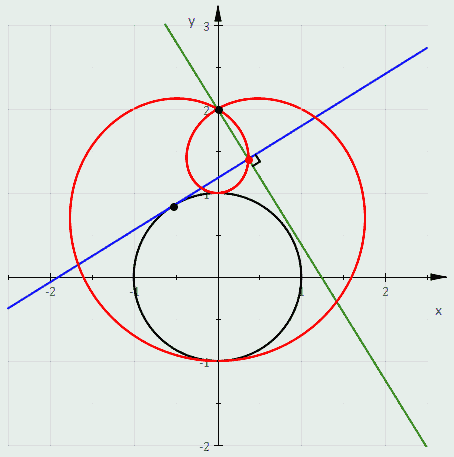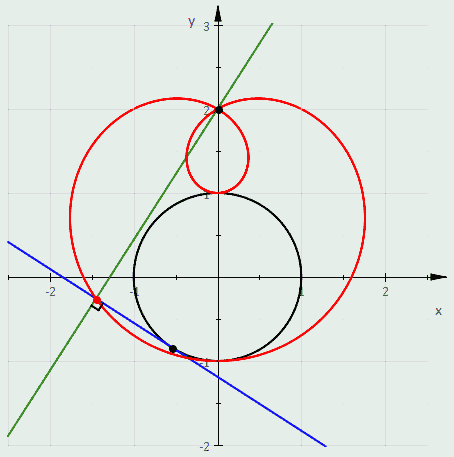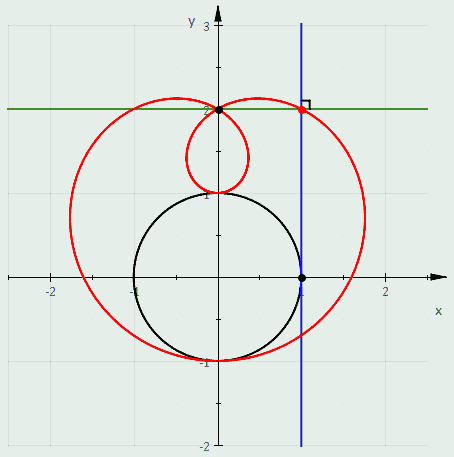
Quando C é uma circunferência a discussão acima mostra que as definições seguintes of a limaçon são equivalentes:

• É o pedal da circunferência.
• É o envelope da circunferência cujo diametro tem um ponto final em um ponto fixo e o ontro ponto final que percorre a circunferência.

Pedals of some specific curves are:^[6]

Curva	Equação	Ponto de pedal	Curva Pedal
Circunferência		Ponto da Circunferência	Cardioid
Circunferência		Qualquer Ponto	Limaçon
Parábola		Foco	A reta tangente no vértice
Parábola		Vértice	Cissoide of Diocles
Conica Central		Foco	Circunferência auxiliar
Cônica Central	${\displaystyle {\frac {x^{2}}{a^{2}}}\pm {\frac {y^{2}}{b^{2}}}=1}$	Centro	${\displaystyle {a^{2}}\cos ^{2}\theta \pm {b^{2}}\sin ^{2}\theta =r^{2}}$ (a hippopede)
Hibérbole Retângular		Centro	Lemniscata de Bernoulli
Espiral logarítmical

• Lista de curvas

• J. Edwards (1892). Differential Calculus. London: MacMillan and Co. pp. 161 ff. 
• Benjamin Williamson (1899). An elementary treatise on the differential calculus. [S.l.]: Logmans, Green, and Co. pp. 227 ff. 

• Differential and integral calculus: with applications by George Greenhill (1891) p326 ff. (Google books)
• J. Dennis Lawrence (1972). A catalog of special plane curves. [S.l.]: Dover Publications. p. 60. ISBN 0-486-60288-5 
• "Note on the Problem of Pedal Curves" by Arthur Cayley

• Weisstein, Eric W. «Pedal Curve». MathWorld (em inglês) 
• Weisstein, Eric W. «Contrapedal Curve». MathWorld (em inglês) 
• Weisstein, Eric W. «Orthotomic». MathWorld (em inglês) 
• "Podaire d'une Courbe" at Encyclopédie des Formes Mathématiques Remarquables