ボンネゼンの不等式

ボンネゼンの不等式 （ボンネゼンのふとうしき、英: Bonnesen's inequality）またはボンネゼンの定理はジョルダン曲線の外接円と内接円、面積、周長に関する不等式である。ユークリッド平面における等周不等式より強力である^[1][2][3]。

具体的には、平面上の単純な閉曲線${\displaystyle S}$の周長を${\displaystyle L}$、面積を${\displaystyle A}$、内接円と外接円の半径をそれぞれ${\displaystyle r,R}$とする。トミー・ボンネゼンは次の不等式を証明した^{[4][註 1]}。 $${\displaystyle \pi ^{2}(R-r)^{2}\leq L^{2}-4\pi A.}$$右辺の${\displaystyle L^{2}-4\pi A}$は"isoperimetric defect"として知られる^[1]。

レヴナーのトーラス不等式（英語版）におけるisosystolic defectはボンネゼンの不等式のisoperimetric defectのシストリック（英語版）な類似物である^[5]。

次の証明はヒューゴ・ハドヴィッガーに帰せられる^[6]。原点中心、半径tの円を${\displaystyle tB}$とする。また、関数${\displaystyle {\text{Area}}(x)}$を閉集合xの面積とする。

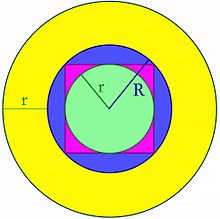
内接円${\displaystyle rB}$と外接円${\displaystyle C}$の半径がそれぞれ${\displaystyle r,R}$である凸コンパクト集合${\displaystyle S}$を考える。図1では、${\displaystyle S}$を紫色の正方形、内接円を緑色、外接円を青色で示してある。${\displaystyle S}$に含まれず、${\displaystyle C}$に含まれる部分を${\displaystyle Z}$とする。ミンコフスキー和${\displaystyle Z+rB}$の面積と半径${\displaystyle r+R}$の円（図1,黄）について

$${\displaystyle {\text{Area}}(Z+rB)=\pi (r+R)^{2}}$$

が成立する。

次に内接円、外接円の中心を通る直線Δで${\displaystyle Z}$を半分に切断する。上の部分を${\displaystyle Z_{s}}$とする。${\displaystyle Z_{s},rB}$のミンコフスキー和は半径${\displaystyle r+R}$の半円板と図2の様な薄黄色の部分の和集合になる。l₁,l₂を${\displaystyle Z}$とΔの2つの交わる部分の長さとして次の式が成立する。 $${\displaystyle {\text{Area}}(Z_{s}+rB)={\frac {1}{2}}\pi (r+R)^{2}+(l_{1}+l_{2})r+\pi r^{2}}$$ この等式にミンコフスキー・シュタイナーの公式を用いて値を評価する。ただし${\displaystyle Z_{s}}$は凸集合ではないため、右辺は極限値とはならない。 $${\displaystyle {\text{Area}}(Z_{s}+rB)={\frac {1}{2}}\pi (r+R)^{2}+(l_{1}+l_{2})r+\pi r^{2}\leq {\text{Area}}(Z_{s})+(\pi R+l_{1}+l_{2}+p_{s})r+\pi r^{2}}$$ ここで${\displaystyle p_{s}}$は、${\displaystyle S}$上部の周長。 下部についても同様にした式と、この式を辺々加えて $${\displaystyle \pi (r+R)^{2}+2(l_{1}+l_{2})r+2\pi r^{2}\leq {\text{Area}}(Z)+2\pi rR+2(l_{1}+l_{2})r+pr+2\pi r^{2}}$$ $${\displaystyle \pi (r+R)^{2}+\leq {\text{Area}}(Z)+2\pi rR+pr}$$ ここでpは${\displaystyle S}$の周長。また、${\displaystyle Z}$の面積は外接円板と${\displaystyle S}$の面積aの差に等しいので、 $${\displaystyle \pi (r+R)^{2}\leq \pi R^{2}-a+2\pi Rr+pr}$$ $${\displaystyle \therefore a-pr+\pi r^{2}\leq 0.}$$

これは面積${\displaystyle S+tB}$についての2次多項式${\displaystyle f(t)=\pi t^{2}-pt+a}$に、内接円半径${\displaystyle r}$を代入した値が負になることを意味する^[7]。

上記と全く同様の議論で、外接円半径${\displaystyle R}$についても同様の結論を得る。

$${\displaystyle a-pR+\pi R^{2}\leq 0.}$$

この2つの不等式より、さらに次の不等式が成立する。 $${\displaystyle {\frac {p-{\sqrt {p^{2}-4\pi a}}}{2\pi }}\leq r\leq R\leq {\frac {p+{\sqrt {p^{2}-4\pi a}}}{2\pi }}.}$$

これを変形して、 $${\displaystyle R-r\leq {\frac {\sqrt {p^{2}-4\pi a}}{\pi }}}$$ $${\displaystyle \therefore p^{2}-4\pi a\geq \pi ^{2}(R-r)^{2}.}$$