Podaria

In geometria, la podaria di un curva rispetto ad un punto ${\displaystyle P}$ detto polo è il luogo geometrico formato dalle proiezioni di ${\displaystyle P}$ sulle rette tangenti alla curva; tali proiezioni sono anche i piedi delle normali alle rette tangenti alla curva passanti per il polo stesso (da cui il termine podaria). La curva originaria è detta anche antipodaria.

Siano date le equazioni parametriche della curva ${\displaystyle \Gamma }$:

${\displaystyle \left\{{\begin{matrix}x&=&f(t)\\y&=&g(t),\end{matrix}}\right.}$

dove ${\displaystyle f}$ e ${\displaystyle g}$ sono due funzioni derivabili su un intervallo ${\displaystyle I\in \mathbb {R} }$. La tangente di ${\displaystyle \Gamma }$ nel suo punto ${\displaystyle \left(f(t),g(t)\right)}$ ha equazione

${\displaystyle y-g(t)={\frac {g^{\prime }(t)}{f^{\prime }(t)}}\left(x-f(t)\right).}$

La proiezione di ${\displaystyle P\left(x_{0},y_{0}\right)}$ sulla tangente si trova sulla retta perpendicolare a questa e passante per ${\displaystyle P}$:

${\displaystyle y-y_{0}=-{\frac {f^{\prime }(t)}{g^{\prime }(t)}}\left(x-x_{0}\right).}$

Intersecando queste due rette si ottiene il generico punto della podaria, che ha le seguenti equazioni parametriche:

${\displaystyle \left\{{\begin{matrix}x&=&{\frac {x_{0}f^{\prime 2}(t)+(y_{0}-g(t))f^{\prime }(t)g^{\prime }(t)+f(t)g^{\prime 2}(t)}{f^{\prime 2}(t)+g^{\prime 2}(t)}}\\y&=&{\frac {g(t)f^{\prime 2}(t)+(x_{0}-f(t))g^{\prime }(t)f^{\prime }(t)+y_{0}g^{\prime 2}(t)}{f^{\prime 2}(t)+g^{\prime 2}(t)}},\end{matrix}}\right.}$

Utilizzando l'equazione sopra descritta si possono calcolare alcuni casi significativi di podaria.

La podaria di una circonferenza è la lumaca di Pascal.

Per dimostrarlo, si considera una circonferenza passante per l'origine di raggio 1 e centro nel punto ${\displaystyle (1,0)}$, di equazioni parametriche:

${\displaystyle \left\{{\begin{matrix}x&=&1+\cos t\\y&=&\sin t.\end{matrix}}\right.}$

Possiamo limitarci a considerare i poli ${\displaystyle P(a,0)}$, posti sull'asse delle ascisse, con ${\displaystyle a\leq 1}$. Le equazioni della podaria sono allora:

${\displaystyle \left\{{\begin{matrix}x&=&\cos t(1+\cos t)+a\sin ^{2}t=a+\cos t+(1-a)\cos ^{2}t\\y&=&\sin t(1+\cos t)-a\sin t\cos t=\sin t+(1-a)\sin t\cos t.\end{matrix}}\right.}$

I casi possibili sono:

• ${\displaystyle P}$ è il centro della circonferenza: la podaria è la circonferenza stessa;
• ${\displaystyle P}$ è interno alla circonferenza: la podaria è senza nodi; se P dista dal centro meno di metà raggio, la podaria racchiude una regione convessa, altrimenti una regione concava;
• ${\displaystyle P}$ è sulla circonferenza: la podaria è una cardioide;
• ${\displaystyle P}$ è esterno alla circonferenza: la podaria è una curva intrecciata.

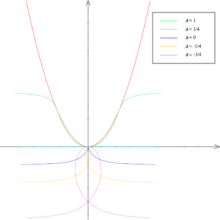
Consideriamo la parabola di equazione ${\displaystyle y=x^{2}}$; le sue equazioni parametriche sono ${\displaystyle x=t}$ e ${\displaystyle y=t^{2}}$; dalla formula generale si ricavano le equazioni della podaria per un polo ${\displaystyle P(0,a)}$ che giace sull'asse della parabola:

${\displaystyle \left\{{\begin{matrix}x&=&{\frac {2t(a+t^{2})}{1+4t^{2}}}\\y&=&{\frac {t^{2}(4a-1)}{1+4t^{2}}}.\end{matrix}}\right.}$

Alcune podarie notevoli sono:

• ${\displaystyle a=1/4}$: il polo coincide con il fuoco della parabola; la podaria è l'asse delle ascisse;
• ${\displaystyle a=0}$: il polo coincide con il vertice della parabola; la podaria è una cissoide di Diocle;
• ${\displaystyle a=-3/4}$: il polo è il simmetrico del fuoco rispetti alla direttrice; la podaria è la trisettrice di Mac Laurin.

• Evoluta di una curva

• Wikimedia Commons contiene immagini o altri file su Podaria

• (ES) Costruzione della podaria di una circonferenza, su matematicas.net (archiviato dall'url originale il 10 marzo 2007).
• Una applet interattiva sulla podaria della parabola, su xoomer.alice.it.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica