En théorie des graphes, un graphe partitionnable[1],[2] est un type particulier de graphe.
Définitions
Partition d'un entier
Soit  un entier strictement positif, une partition de
un entier strictement positif, une partition de  est une suite d’entiers
est une suite d’entiers  telle que :
telle que :



k-partition d'un entier
Une  -partition de
-partition de  est une partition de
est une partition de  possédant
possédant  éléments.
éléments.
S-partition d'un graphe
Soit  un graphe simple où :
un graphe simple où :
 est l'ensemble non vide des sommets de G.
est l'ensemble non vide des sommets de G. est l'ensemble des arêtes de G, c'est-à-dire un sous-ensemble de l'ensemble des parties à deux éléments de
est l'ensemble des arêtes de G, c'est-à-dire un sous-ensemble de l'ensemble des parties à deux éléments de  .
.
Soit  une partition de
une partition de  (le nombre de sommets du graphe G).
(le nombre de sommets du graphe G).
 est dit admettre une
est dit admettre une  -partition s'il existe une partition
-partition s'il existe une partition  de
de  telle que :
telle que :

![{\displaystyle \forall i\in \left\{1,...,m\right\},G[V_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02ace65441d4f99ffb7d67b682e0971360f34738) est un graphe connexe.
est un graphe connexe.
L'ensemble  est alors dit être une partition de
est alors dit être une partition de  induite par
induite par  .
.
Graphe partitionnable
Un graphe  est dit partitionnable s'il admet une
est dit partitionnable s'il admet une  -partition pour toute partition
-partition pour toute partition  de
de  .
.
Graphe k-partitionnable
Un graphe  est dit
est dit  -partitionnable s'il admet une
-partitionnable s'il admet une  -partition pour toute
-partition pour toute  -partition
-partition  de
de  .
.
Exemples
k-partition de n
- Une
 -partition de
-partition de  est
est  .
. - Une
 -partition de
-partition de  est
est  .
. - Une
 -partition de
-partition de  est
est  .
.
S-partition de G
Soit le graphe  tel que :
tel que :


représenté ci-dessous par :
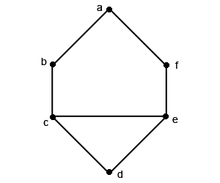
 .
.  admet 3 partitions de 6 possibles :
admet 3 partitions de 6 possibles :  ,
,  et
et  (en considérant que l'ordre des différentes suites n'a pas d'importance).
(en considérant que l'ordre des différentes suites n'a pas d'importance).
Ces trois partitions de l'entier 6 peuvent être appliquées respectivement pour partager le graphe  comme ceci :
comme ceci :
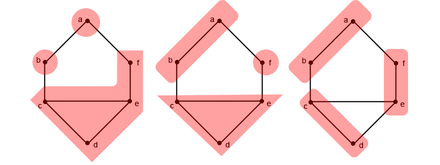
Il existe bien d'autres façons d'appliquer ces 3 partitions sur ce graphe. Le schéma ci-dessus est une des représentations possibles.
Notes et références
- ↑ (en) « Graphclass: partitionable », Information System on Graph Classes and their Inclusions (consulté le ).
- ↑ Nicolas Trotignon, Graphes parfaits : Structure et algorithmes (Thèse), Université Grenoble I, Joseph Fourier, (arXiv 1309.0119.pdf).
 Portail de l'informatique théorique
Portail de l'informatique théorique


 Portail de l'informatique théorique
Portail de l'informatique théorique 














![{\displaystyle \forall i\in \left\{1,...,m\right\},G[V_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02ace65441d4f99ffb7d67b682e0971360f34738)
























