Fonction demi-exponentielle

En mathématiques, une fonction semi-exponentielle est une racine carrée fonctionnelle d'une fonction exponentielle. Autrement dit, une fonction ${\displaystyle f}$ telle que ${\displaystyle f}$ composée avec elle-même donne une fonction exponentielle^[1],[2]: $${\displaystyle f{\bigl (}f(x){\bigr )}=ab^{x},}$$ pour certaines constantes ${\displaystyle a}$ et ${\displaystyle b}$.

Si une fonction ${\displaystyle f}$ est définie à l'aide des opérations arithmétiques standard, de l'exponentiation, des logarithmes et des constantes réelles, alors ${\displaystyle f{\bigl (}f(x){\bigr )}}$ est soit sous-exponentielle, soit super-exponentielle^[3]. Ainsi, une fonction L de Hardy ne peut pas être semi-exponentielle.

Toute fonction exponentielle peut être écrite comme l'auto-composition ${\displaystyle f(f(x))}$ pour une infinité de choix possibles de ${\displaystyle f}$. En particulier, pour chaque ${\displaystyle A}$ dans l'intervalle ouvert ${\displaystyle ]0,1[}$ et pour toute fonction continue strictement croissante ${\displaystyle g}$ depuis ${\displaystyle [0,A]}$ sur ${\displaystyle [A,1]}$, il existe un prolongement de cette fonction vers une fonction continue strictement croissante ${\displaystyle f}$ sur les nombres réels tels que ${\displaystyle f{\bigl (}f(x){\bigr )}=\exp x}$^[4]. La fonction ${\displaystyle f}$ est l'unique solution de l'équation fonctionnelle$${\displaystyle f(x)={\begin{cases}g(x)&{\mbox{si }}x\in [0,A],\\\exp g^{-1}(x)&{\mbox{si }}x\in ]A,1],\\\exp f(\ln x)&{\mbox{si }}x>1,\\\ln f(\exp x)&{\mbox{si }}x<0.\\\end{cases}}}$$

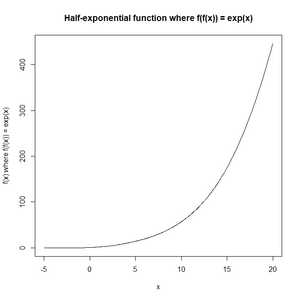
Un exemple simple, qui conduit à ${\displaystyle f}$ avec une dérivée continue partout, consiste à prendre ${\displaystyle A={\tfrac {1}{2}}}$ et ${\displaystyle g(x)=x+{\tfrac {1}{2}}}$, donnant$${\displaystyle f(x)={\begin{cases}\ln \left(\mathrm {e} ^{x}+{\tfrac {1}{2}}\right)&{\mbox{si }}x\leq -\ln 2,\\\mathrm {e} ^{x}-{\tfrac {1}{2}}&{\mbox{si }}{-\ln 2}\leq x\leq 0,\\x+{\tfrac {1}{2}}&{\mbox{si }}0\leq x\leq {\tfrac {1}{2}},\\\mathrm {e} ^{x-1/2}&{\mbox{si }}{\tfrac {1}{2}}\leq x\leq 1,\\x{\sqrt {\mathrm {e} }}&{\mbox{si }}1\leq x\leq {\sqrt {\mathrm {e} }},\\\mathrm {e} ^{x/{\sqrt {\mathrm {e} }}}&{\mbox{si }}{\sqrt {\mathrm {e} }}\leq x\leq \mathrm {e} ,\\x^{\sqrt {\mathrm {e} }}&{\mbox{si }}\mathrm {e} \leq x\leq \mathrm {e} ^{\sqrt {\mathrm {e} }},\\\mathrm {e} ^{x^{1/{\sqrt {\mathrm {e} }}}}&{\mbox{si }}\mathrm {e} ^{\sqrt {\mathrm {e} }}\leq x\leq \mathrm {e} ^{\mathrm {e} },\ldots \\\end{cases}}}$$

Les fonctions demi-exponentielles sont utilisées dans la théorie de la complexité informatique pour les taux de croissance « intermédiaires » entre polynôme et exponentiel. ^[1] Une fonction ${\displaystyle f}$ croît au moins aussi vite qu'une fonction demi-exponentielle (sa composition avec elle-même croît de façon exponentielle) si elle est non décroissante et ${\displaystyle f^{-1}(x^{C})=o(\log x)}$, pour tout ${\displaystyle C>0}$^[5].

• Fonction itérée
• Équation de Schröder
• Équation d'Abel (en)

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Half-exponential function » (voir la liste des auteurs).

• (en) Does the exponential function have a (compositional) square root?
• (en) "Closed-form" functions with half-exponential growth

• Portail de l'analyse