Simsonin suora

Simsonin suora on geometriassa kolmioon ja ympyrään liittyvä seuraava tulos. Ne kolmion eri sivuilla, tai sivujen jatkeilla, olevat pisteet, joiden etäisyys kolmiota ympäröivän ympyrän kehäpisteelle on lyhin, sijaitsevat samalla suoralla.^[1]

Sama asia voidaan ilmaista toisinkin. Kolmiota ympäröivältä ympyrän kehältä valitaan piste P, josta vedetään normaalit kullekin kolmion sivusuoralle, eli sivulle tai sen jatkeelle. Normaalien ja sivusuorien leikkauspisteet ovat keskenään kollineaariset.^[1]

Niiden pisteiden ura, joiden normaalien kantapisteet kolmion sivusuorilla ovat kollineaariset, muodostavat ympyrän, joka kulkee kolmon kärkien kautta eli ympäröi kolmion. Teoreema on siten molempisuuntainen.^[1]

Pisteen P normaalit kolmion sivuille voidaan tulkita pedaaleiksi eli kohtisuoriksi, joiden kohtaamispisteitä kutsutaan siksi kantapisteiksi (tai projektiopisteiksi). Pistettä P kutsutaan silloin pedaalipisteeksi ja kantapisteiden muodostamaa kolmiota kutsutaan pedaaliseksi kolmioksi.

Kun pedaalipiste on kolmion sisällä, on pedaalikolmio useimmiten teräväkulmainen kolmio. Kun pedaalipiste siirretään kolmion kehän yli sen ulkopuolella, muttuu pedaalikolmio tylppäkulmaiseksi kolmioksi. Lopulta pedaalikolmion yksi kärki yhtyy vastaiseen sivuun, kun pedaalipiste P on kolmiota ympäröivällä ympyrällä, jolloin kolmion on muuttunut janaksi (Simsonin suora).^[2]

• Kun piste P sijaitsee kolmion kärjessä, muodostuva Simsonin suora on vastaisen sivun normaali, jolloin se yhtyy kolmion korkeusjanaan.^[1]
• Kun Simsonin suora yhtyy kolmion sivun kanssa, sijaitsevat piste P ja kolmion vastainen kärki ympäröivän ympyrän yhteisellä halkaisijalla.^[1]
• Simsonin suora puolittaa ortokeksuksen O ja kehäpisteen P yhdistävän janan. Tämä keskipiste on myös yhdeksän pisteen ympyrällä.^[1]
• Jos valitaan ympyrältä kaksi pistettä P ja P' siten, että ne sijaitsevat ympyrän vastakkaisilla puolilla, on niiden Simsonin suorat kohtisuorassa toisiaan vastaan. Leikkauspiste sijaitsee yhdeksän pisteen ympyrällä.^[1]
• Jos valitaan kaksi kehäpistettä P ja P' mielivaltaisesti, on niiden Simsonin suorien välinen kulma puolet pisteisiin P ja P' päättyvien ympyrän säteiden välisestä keskuskulmasta.^[1]
• Kaikkien pisteiden P Simsonin suorien pyyhkäisemä alue muodostaa deltoidin. Deltoidin pinta-ala on puolet ympäröivän ympyrän pinta-alasta. Referenssikolmion sivut ovat deltoidin tangentteja.^[1]

• 
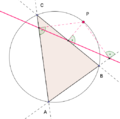  Simsonin suora ja normaalien kantapisteet.
• 
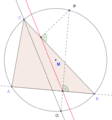  Yhdensuuntainen jana Simsonin suoran kanssa.
• 
  Eri pedaalipisteiden Simsonin suorien välinen kulma on puolet pedaalipisteiden keskuskulmaan verrattuna.
• 
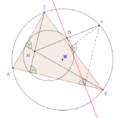  Simsonin suora jakaa puolittaa ortokeskuksen ja pedaalipisteen välisen janan.
• 
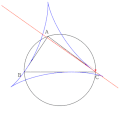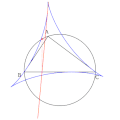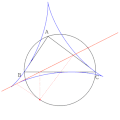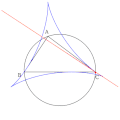  Simsonin suora (punainen) on tangenttina Steinerin deltoidille (sininen).

Kollineaarisuus voidaan todistaa osoittamalla, että kantapisteet ovat linjassa eli ${\displaystyle \scriptstyle \measuredangle NMP+\measuredangle PML=180^{\circ }}$ (merkinnät kuvassa).

1. Ympyrän kehällä olevat neljä pistettä P, C, A ja B voidaan yhdistää sykliseksi nelikulmioksi. Sille pätee, että vastakkaisten kulmien summa on aina 180°. Erityisesti ${\displaystyle \scriptstyle \measuredangle PBA+\measuredangle ACP=180^{\circ }}$ ja vielä huomataan, että ${\displaystyle \scriptstyle \measuredangle PBA=\measuredangle PBN}$.
2. Toinen nelikulmio voidaan muodostaa pisteistä P, M, N ja B. Tämä nelikulmio on myös syklinen, koska Thaleen lauseen mukaan janan PB vastaiset kulmat ${\displaystyle \scriptstyle \measuredangle BNP=90^{\circ }}$ ja ${\displaystyle \scriptstyle \measuredangle BMP=90^{\circ }}$ syntyvät näitä ympäröivän ympyrän takia. Tämän ympyrän halkaisija on siten jana PB. Kun valitaan vastakkaiset kulmat sopivasti, saadaan ${\displaystyle \scriptstyle \measuredangle PBN+\measuredangle NMP=180^{\circ }}$.
3. Kohdista 1. ja 2. seuraa, että on olemassa yhtäsuuruiset kulmat ${\displaystyle \scriptstyle \measuredangle NMP=\measuredangle PBN=\measuredangle ACP}$.
4. Tarvitaan vielä edellisen nelikulmion viereinen nelikulmio, joka syntyy yhdistämällä pisteet P, L, C ja M. Tämäkin ympyrä on syklinen, koska siinä on halkaisijan PC molemmilla puolilla suorat kulmat ${\displaystyle \scriptstyle \measuredangle CLP}$ ja ${\displaystyle \scriptstyle \measuredangle PMC}$. Nelikulmion jännettä PL vastaan aukeaa kaksi samansuuruista kehäkulmaa ${\displaystyle \scriptstyle \measuredangle PML=\measuredangle PCL}$, joista jälkimmäisen vieruskulmalle ${\displaystyle \scriptstyle \measuredangle ACP}$ pätee ${\displaystyle \scriptstyle \measuredangle PCL=180^{\circ }-\measuredangle ACP}$.

Nyt voidaan laske kulmien summa (suluissa päättelyyn johtavat tulokset)

${\displaystyle \measuredangle NMP+\measuredangle PML\,{\overset {3.}{=}}\,\measuredangle ACP+\measuredangle PML\,{\overset {4.}{=}}\,\measuredangle ACP+(180^{\circ }-\measuredangle ACP)=180^{\circ }}$.

Tämä on alkuperäinen väite, joka on nyt osoitettu todeksi.

Simsonin suoran nimesi Poncelet Robert Simsonin (1687–1768) kunniaksi. Simsonin julkaisuissa sitä ei kuitenkaan esiinny ja ensimmäinen tunnettu julkaisu teoreemasta on William Wallacelta vuonna 1797. Tämän vuoksi teoreeman käänteistä muotoa saatetaan kutsua Wallace-Simson-suoraksi.^[3][1]