Variables de Mandelstam

Las variables de Mandelstam en física teórica son cantidades numéricas que codifican la energía, momento y ángulos de las partículas que participan en una colisión de manera invariante Lorentz. Se emplean principalmente en procesos de dispersión de dos partículas para dar otras dos partículas. Fueron introducidas por el físico Stanley Mandelstam en 1958.

Si se toma la métrica de Minkowski como ${\displaystyle \mathrm {diag} (1,-1,-1,-1)}$, las variables de Mandelstam ${\displaystyle s,t,u}$ se definen como

• ${\displaystyle s=(p_{1}+p_{2})^{2}=(p_{3}+p_{4})^{2}\,}$
• ${\displaystyle t=(p_{1}-p_{3})^{2}=(p_{2}-p_{4})^{2}\,}$
• ${\displaystyle u=(p_{1}-p_{4})^{2}=(p_{2}-p_{3})^{2}\,}$

donde p₁ y p₂ son los cuadrimomentos de las partículas incidentes, y p₃ y p₄ los cuadrimomentos de las partículas salientes, y se emplean unidades relativistas (c=1).

${\displaystyle s}$ es el cuadrado de la energía en el sistema de referencia del centro de masas (masa invariante), y ${\displaystyle t}$ es el cuadrado de la transferencia de cuadrimomento.

Las letras ${\displaystyle s,t,u}$ también se emplean en los términos canal s (canal espacial), canal t (canal temporal) y canal u. Estos canales representan los diagramas de Feynman que describen procesos de dispersión en los que se intercambia una partícula virtual cuyo cuadrimomento al cuadrado es igual a ${\displaystyle s,t,u}$, respectivamente.

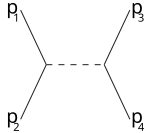
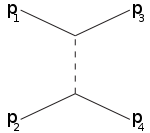
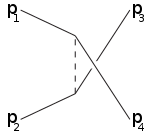
canal s	canal t	canal u

Por ejemplo, el canal s corresponde a las partículas 1 y 2 (partículas incidentes) uniéndose en una partícula intermedia que finalmente da lugar a las partículas 3 y 4: el canal s es la única forma en la que se pueden descubrir resonancias y partículas inestables si sus vidas medias son suficientemente largas para poder ser detectadas. El canal t representa un proceso en el que la partícula 1 emite una partícula intermedia y se transforma en la partícula 3, mientras que la partícula 2 absorbe la partícula intermedia y se transforma en la partícula 4. El canal u es el canal t intercambiando los papeles de las partículas 3 y 4.

En el límite relativista, la velocidad y el momento son elevados, por lo que usando la relación de energía-momento relativista, la energía es aproximadamente la norma del momento (${\displaystyle E^{2}=\mathbf {p} \cdot \mathbf {p} +{m_{0}}^{2}}$ pasa a ser ${\displaystyle E^{2}\approx \mathbf {p} \cdot \mathbf {p} }$ ). La masa en reposo de las partículas se considera despreciable.

Por ejemplo,

${\displaystyle s=(p_{1}+p_{2})^{2}=p_{1}^{2}+p_{2}^{2}+2p_{1}\cdot p_{2}\approx 2p_{1}\cdot p_{2}\,}$

ya que ${\displaystyle p_{1}^{2}=m_{1}^{2}}$ y ${\displaystyle p_{2}^{2}=m_{2}^{2}.}$

Por lo tanto,

${\displaystyle s\approx \,}$	${\displaystyle 2p_{1}\cdot p_{2}\approx \,}$	${\displaystyle 2p_{3}\cdot p_{4}\,}$
${\displaystyle t\approx \,}$	${\displaystyle -2p_{1}\cdot p_{3}\approx \,}$	${\displaystyle -2p_{2}\cdot p_{4}\,}$
${\displaystyle u\approx \,}$	${\displaystyle -2p_{1}\cdot p_{4}\approx \,}$	${\displaystyle -2p_{3}\cdot p_{2}\,}$

Las tres variables de Mandelstam no son independientes entre sí, ya que su suma es

${\displaystyle s+t+u=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}\,}$

donde ${\displaystyle m_{i}}$ es la masa de la partícula ${\displaystyle i}$.

Para demostrar la expresión anterior emplearemos los siguientes hechos:

• El cuadrado del cuadrimomento de una partícula es el cuadrado de su masa,

${\displaystyle p_{i}^{2}=m_{i}^{2}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (1)\,}$

• El cuadrimomento es una cantidad conservada,

${\displaystyle p_{1}+p_{2}=p_{3}+p_{4}\,}$

${\displaystyle p_{1}=-p_{2}+p_{3}+p_{4}\quad \quad \quad \quad \quad \quad \quad (2)\,}$

Por lo tanto,

${\displaystyle s=(p_{1}+p_{2})^{2}=p_{1}^{2}+p_{2}^{2}+2p_{1}\cdot p_{2}\,}$

${\displaystyle t=(p_{1}-p_{3})^{2}=p_{1}^{2}+p_{3}^{2}-2p_{1}\cdot p_{3}\,}$

${\displaystyle u=(p_{1}-p_{4})^{2}=p_{1}^{2}+p_{4}^{2}-2p_{1}\cdot p_{4}\,}$

Sumando las tres variables y empleando las masas de las partículas se tiene que

${\displaystyle s+t+u=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}+2p_{1}^{2}+2p_{1}\cdot p_{2}-2p_{1}\cdot p_{3}-2p_{1}\cdot p_{4}\,}$

La suma de los últimos cuatro términos es cero debido a la conservación del cuadrimomento,

${\displaystyle 2p_{1}^{2}+2p_{1}\cdot p_{2}-2p_{1}\cdot p_{3}-2p_{1}\cdot p_{4}=2p_{1}\cdot (p_{1}+p_{2}-p_{3}-p_{4})=0\,}$

Por lo que finalmente,

${\displaystyle s+t+u=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}\,}$

• Diagrama de Feynman
• Dispersión Compton

• Mandelstam, S. (1958). «Determination of the Pion-Nucleon Scattering Amplitude from Dispersion Relations and Unitarity». Physical Review 112 (4): 1344. Bibcode:1958PhRv..112.1344M. doi:10.1103/PhysRev.112.1344. Archivado desde el original el 28 de mayo de 2000. 
• Halzen, Francis; Martin, Alan (1984). Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2. 
• Perkins, Donald H. (2000). Introduction to High Energy Physics (4th edición). Cambridge University Press. ISBN 0-521-62196-8.